evmn.github.io

一道数学题

Mathematics and Plausible Reasoning第一章有个数学题目：

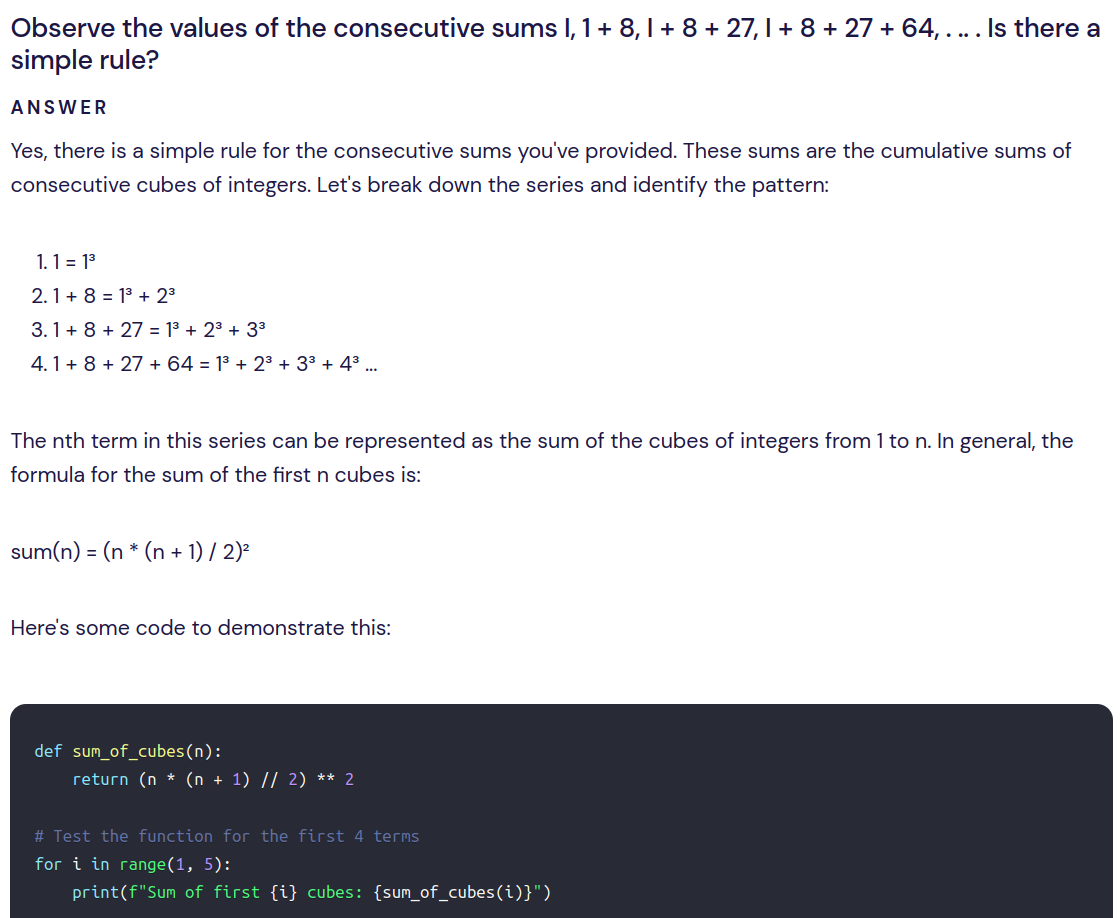
Observe the values of the consecutive sums
1,
1 + 8,
1 + 8 + 27,
1 + 8 + 27 + 64,
. .. .
Is there a simple rule?

昨天晚上一直在思考这个问题，最近几年我比较倾向于无纸化办公，但是我发现不用纸笔很难准确描述我的想法，因为我发现的规律是这样的：

\[\sum_{n=1}^k n^3 = \left( \sum_{n=1}^k n \right)^2 = \left( \frac{k\left( k+1 \right)}{2} \right)^2\]

之后，我想要从几何的角度更直观的认识这个规律，于是我努力想像把三维正方体在平面展开的样子，于是就有了这张图。

\[n^{3}=n^{2}+2n\left(\sum_{k=0}^{n-1}k\right)=n^{2}+2n\frac{\left( n-1 \right)n}{2}\]

1³ = (1)²
1³ + 2³ = (1 + 2)²
1³ + 2³ + 3³ = (1 + 2 + 3)²
1³ + 2³ + 3³ + 4³ = (1 + 2 + 3 + 4)²
1³ + 2³ + 3³ + 4³ + 5³ = (1 + 2 + 3 + 4 + 5)²

我又在phind考验了一下GPT-4，发现勾选Expert和Creative后，给出的答案非常让人满意。